QUANTUM MANY BODY SISTEMS

QUANTUM MANY BODY SYSTEMS

• STRONGLY CORRELATED SYSTEMS

In the last decades, experiments have led to the possibility of studying in the laboratories new quantum effects and phases of matter that are characteristic of low-dimensional strongly correlated systems and have been considered for many years, in some respects, only a theoretical divertissement. As examples, we may recall:

macroscopic quantum coherence effects, that can be seen both in fermionic (high Tc superconductors ) and in bosonic systems (Bose-Einstein condensation)

topological order phases, which are described by non-local order parameters, often found in spin systems

quantum number fractionalization, for solitons -as found long ago in polyacetilene rings or recently in layers of graphene- or for anionic excitations in fractional Hall systems

entanglement, which has been proved to be a fundamental property of the ground state of many strongly correlated systems (spin chains, Josephson junctions, optical lattices) opening the way to the study of novel quantum devices.

These new developments have become possible thanks to the experimental advances in the realm of micro- and nano-physics, the last (but not least) being represented by the striking ability to manipulate ultracold atoms and molecules in optical lattices. Now it is possible to build such systems to simulate a variety of physical models that are not accessible by means of standard condensed matter or optical systems. They include both bosonic and fermionic systems, in 1, 2 or 3 d, with interactions that can be tuned with great precision over a large range of values, making these systems excellent examples of “quantum simulators”.

• THEORY OF QUANTUM MANY BODY SYSTEMS

From a theoretical point of view, low-dimensional strongly correlated quantum systems have become an autonomous branch of research, also thanks to the great wealth of theoretical techniques that are available, in particular in dimension d=2 for classical models, or d=1 for their quantum counterpart. A common feature of all these models is the fact that they cannot be treated perturbatively, due to the interplay between the role of the strong interactions and that of the low dimensionality. The understanding of 1d strongly correlated systems rests on the possibility of complementing more standard Many Body Theory (MBT) approaches with Quantum Field Theory (QFT) ones, i.e. of using a combination of theoretical methods that include analytical techniques such as Conformal Field Theories (CFT) and Integrable Systems (IS). This was first suggested for the Heisenberg chain in a seminal paper by Haldane -where it was shown that the emergence of a topological term could account for the difference in the behaviour of half-integer and integer spin, and soon generalized to a variety of models, that include almost 1d systems as well. Let us also recall that in 1d the phenomena emerging in systems of spin ½ particles, fermions and bosons are strictly inter-related, since one may rely, on one side, on the Jordan-Wigner transformation -that allows to rewrite spin ½ operators in terms of fermionic ones- and, on the other, on bozonization techniques. The analytical methods presented above may be complemented by numerical ones. Among the latter, it is worth mentioning the Density Matrix Renormalization Group (DMRG) algorithm, originally proposed by S.R. White as an efficient method to study 1d strongly correlated quantum systems, which is essentially based on the construction of a renormalization flow in a space of suitably truncated density matrices. In more recent years, there have been several developments of this idea, also in the direction of studying time-dependent or non-equilibrium properties. In many situations, this has led to very satisfactory descriptions of the physics of the investigated models. The literature in this field is wide and it is worth recalling that, in this way, it has been possible to determine with great accuracy the ground state phase diagrams and the corresponding correlation functions for a variety of integrable and non-integrable models, which are characterized by the appearance of quantum phase transitions (QPTs) and of nontrivial ordered phase.

• OUT OF EQUILIBRIUM PROPERTIES

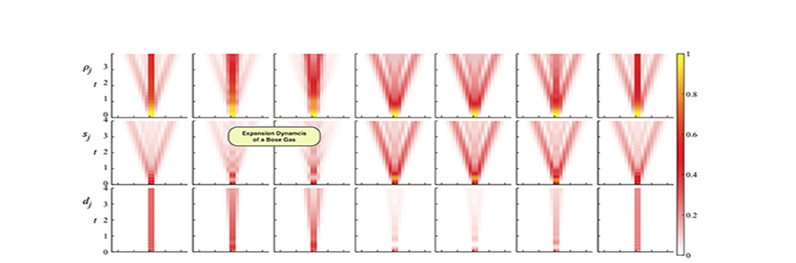
The experimental success in preparing dilute ultracold bosonic and fermionic gases trapped in an optical lattice has also drawn attention to the properties of relaxation to equilibrium, decoherence and of transport. These systems, that may have an important impact on the realization of quantum devices for information and computation technology, are almost ideal from a theoretician's point of view. Thus non-equilibrium dynamics of strongly correlated many body systems has become a topic largely discussed in literature, since -at least in the quantum setting- there are still many open questions, connected to fundamental problems, that lack a complete and satisfactory answer. One may devise different protocols under which to study the out-of-equilibrium dynamics. For example one can ask whether and how an extended system can relax to equilibrium (i.e. to a Gibbs ensamble) after a quench due to a sudden change of the Hamiltonian. Or, one can follow the behavior of the system as the coupling constants in the Hamiltonian are changed with a finite rate. In particular, it is interesting to see what happens when a system is driven across a phase transition between a disordered and an ordered phase, so that topological defects might be generated (Kibble-Zurek mechanism). In these respects, strongly correlated 1d models appear to be an almost inexhaustible source of physical systems where one can try to find an answer to the above mentioned questions, not only because their equilibrium properties are well known but also because they include very flexible situations, with many instances of non-trivial integrable systems and situations where, for example, one can choose to add different kinds of perturbations that may or may not break integrability on lattices and in the continuum.

• ENTANGLEMENT & QUANTUM PHASE TRANSITIONS

In recent years, the notion of entanglement has been proven to be very useful for the analysis of non-trivial phases of both MBT and QFT, becoming a resource not only for quantum information but also for theoreticians working in quantum statistical field theory. In this contest the non-trivial problem of determining a quantity able to quantify the degree of entanglement of a many body system or of a field theory model has attracted much attention, in particular after having realized that it is possible to detect QPTs by looking at the proper entanglement indicators. Restricting the attention to bipartite entanglement, it has been shown that information about phase transitions can be obtained by looking at the reduced density matrix of part of the system, with respect to the rest. This is true for lattice systems as well as for continuum models. More specifically, one can prove that von Neumann and Renyi block entropies as well as the spectrum of the density matrix are ruled by universal laws, their behavior depending only on coefficients such as the central charge and the exponents that characterize the class of universality of the phase transition. Finally, we remark that entanglement indicators (block entropies, adiabatic fidelity, Loschmidt echo, …) can be considered in the study of non-equilibrium properties as well.

• GEOMETRY OF QUANTUM MECHANICS

The non-trivial structure of the space of states of a quantum mechanical model (both for finite and infinite number of degrees of freedom) is at the heart of many interesting phenomena, such as Berry’s phase or entanglement, whose features are only weakly (or at all) dependent on the actual dynamics of the system, being related instead to global topological and geometrical properties. Alternative dynamical descriptions of a system that can be obtained by changing the geometric structures (linearity, hermitean form, ..) of the underlying space of states. In such a framework, one can set the study of some interesting problems such as the one associate to PT-symmetric models or some notions of non-linearity. Also, the geometry of the space of states is also deeply connected to the definition of entanglement indicator and to the theory of quantum information. For example, both on pure and mixed states, one can define the notion of Fisher Tensor: its antisymmetric part gives the so-called KKS symplectic form whose integral yields the magnetic flux associated to the Berry’s phase connections, while its symmetric part yields the FS metric and hence the so called Fisher Information, usually considered when examining optimization problems.

OVERVIEW